
Zadanie Stacja (sta)
Pomóż nam usprawnić bazę zadań!
Stacja
Limit pamięci: 192 MB
W Bajtocji zakończył się pierwszy etap reformy (Został on opisany w zadaniu Koleje z III etapu XIV OI. Znajomość zadania Koleje nie jest jednak w najmniejszym stopniu potrzebna do rozwiązania niniejszego zadania.) sieci kolejowej. Owa sieć składa się z dwukierunkowych odcinków torów łączących stacje kolejowe. Żadne dwie stacje nie są połączone więcej niż jednym odcinkiem torów. Ponadto wiadomo, że z każdej stacji kolejowej da się dojechać do każdej innej dokładnie jedną trasą. Trasa może być złożona z kilku odcinków torów, ale nigdy nie przechodzi przez żadną stację więcej niż raz.
Celem drugiego etapu reformy jest zaplanowanie połączeń kolejowych. Bajtazar liczy na to, że mu w tym pomożesz. Aby uprościć zadanie, Bajtazar postanowił, że:
- jedna ze stacji stanie się wielkim węzłem kolejowym i otrzyma nazwę Bitowice,
- ze wszystkich pozostałych stacji uruchomione zostaną połączenia kolejowe do Bitowic i z powrotem,
- każdy pociąg będzie jeździł między Bitowicami i drugą stacją końcową po jedynej możliwej trasie, zatrzymując się na wszystkich mijanych stacjach.
Pozostaje pytanie o to, która stacja powinna zostać Bitowicami. Postanowiono, że system połączeń powinien być tak zaplanowany, by średni koszt przejazdu między dwiema różnymi stacjami kolejowymi był minimalny. W Bajtocji obowiązują wyłącznie bilety jednorazowe w cenie 1 bajtalara, upoważniające do przejazdu jednym połączeniem na dowolną odległość. Tak więc koszt przejazdu między dwiema konkretnymi stacjami to minimalna liczba połączeń, jakie trzeba wykorzystać, aby przejechać z jednej stacji do drugiej.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia opis sieci kolejowej w Bajtocji,
- wyznaczy stację, która powinna zostać Bitowicami,
- wypisze wynik na standardowe wyjście.
Wejście
W pierwszym wierszu wejścia zapisana jest
jedna liczba całkowita  (
(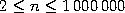 ) -
jest to liczba stacji kolejowych.
Stacje kolejowe są ponumerowane od
) -
jest to liczba stacji kolejowych.
Stacje kolejowe są ponumerowane od 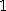 do
do  .
Stacje łączy
.
Stacje łączy 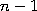 odcinków torów kolejowych.
Są one opisane w kolejnych
odcinków torów kolejowych.
Są one opisane w kolejnych 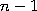 wierszach, po jednym w wierszu.
W każdym z nich są zapisane dwie dodatnie liczby całkowite
wierszach, po jednym w wierszu.
W każdym z nich są zapisane dwie dodatnie liczby całkowite
 oraz
oraz 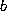 (
(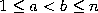 ),
oddzielone pojedynczym odstępem i oznaczające
numery stacji, które łączy dany odcinek torów.
),
oddzielone pojedynczym odstępem i oznaczające
numery stacji, które łączy dany odcinek torów.
Wyjście
W pierwszym i jedynym wierszu wyjścia Twój program powinien wypisać jedną liczbę całkowitą - optymalną lokalizację stacji Bitowice. Jeżeli istnieje więcej niż jedna optymalna odpowiedź, Twój program powinien wypisać dowolną z nich.
Przykład
Dla danych wejściowych:
8 1 4 5 6 4 5 6 7 6 8 2 4 3 4
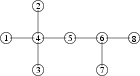
poprawną odpowiedzią jest:
7
Kółka na rysunku reprezentują stacje (liczby w kółkach to numery
stacji), a krawędzie to odcinki torów.
Możliwymi optymalnymi lokalizacjami Bitowic są stacje 7 oraz 8.
W przypadku wyboru dowolnej z nich, średni koszt przejazdu między
różnymi stacjami będzie równy 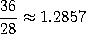 (w przykładzie jest
(w przykładzie jest 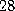 par nieuporządkowanych różnych stacji).
par nieuporządkowanych różnych stacji).
Autor zadania: Marcin Kubica.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English